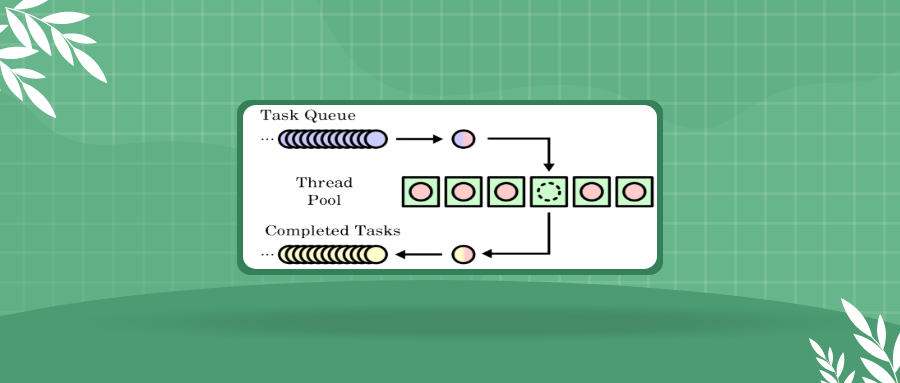
线程池是一种用于管理和重用线程的技术,广泛用于需要大量短生命周期线程的应用场景,如并发任务处理、网络服务和高性能计算等。使用线程池可以有效减少线程创建和销毁的开销,提升系统性能。本文将详细讲解线程池的基本概念、设计原则,并提供一个 C++ 实现的示例。
本文中涉及的C++11特性,不熟悉的话可以查阅C++11新特性文档
1. 线程池的设计线程池的基本思想是预先创建一定数量的线程,并将它们放入一个池中。线程池负责管理线程的生命周期,并将任务分配给空闲线程执行。这样可以避免每次任务执行时都创建和销毁线程的开销。
如果要编写一个线程池,它的组成如下:
线程池管理器:负责创建、销毁线程,维护线程池状态(如空闲线程、忙碌线程)。
任务队列:用于存储待执行的任务。任务通常以函数对象(如 std::function)的形式存储。
工作线程:线程池中的实际线程,它们从任务队列中取出任务并执行。
同步机制:用于保护任务队列和线程池状态的线程安全操作,通常使用互斥锁和条件变量。
在设计线程池时,我们需要考虑以下几个重要原则:
线程池大小管理:
固定大小:线程池中的线程数量固定不变。适用于负载比较稳定 ...
1. 排序的稳定性排序是我们生活中经常会面对的问题,小朋友站队的时候会按照从矮到高的顺序排列;老师查看上课出勤情况时,会按照学生的学号点名;高考录取时,会按照成绩总分降序依次录取等等。那么对于排序它是如何定义的呢?
排序是将一批无序的记录(数据)根据关键字重新排列成有序的记录序列的过程。 在工作和编程过程中我们经常接触的有八种经典的排序算法分别是:
冒泡排序
选择排序
插入排序
希尔排序
快速排序
归并排序
堆排序
基数排序
关于排序还有另一个大家需要掌握的概念就是排序的稳定性。排序的稳定性指的是在排序算法中,如果两个元素的键值相等,排序后它们的相对顺序是否会保持不变。
如果排序算法是稳定的,那么在排序之前和之后,相同键值元素的相对顺序是相同的;
如果排序算法是不稳定的,那么相同键值元素的相对顺序可能会发生变化。
假设我们有一组待排序的对象,其中每个对象有两个属性:键值和姓名。并要求根据键值对每组数据进行排序:
键值
姓名
4
令狐冲
3
任盈盈
4
岳不群
1
杨过
3
小龙女
使用稳定的排序算法(例如插入排序、归并排序、冒泡排序),结果会是 ...
1. 二分搜索概述二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search),是一种在有序数组中查找某一特定元素的搜索算法。
二分搜索是一种高效的查找算法,适用于在已排序的数组中查找特定元素。它的基本思想是通过不断将搜索区间对半分割,从而快速缩小查找范围。
二分搜索每次把搜索区域减少一半,时间复杂度为 O(logn)(n代表集合中元素的个数)。
二分搜索的基本步骤如下:
初始条件:将搜索范围设为数组的整个区间。
查找中间元素:计算当前区间的中间索引。
比较中间元素:将中间元素与目标值进行比较:
如果中间元素等于目标值,查找成功,返回中间索引。
如果中间元素小于目标值,将搜索范围缩小到右半部分。
如果中间元素大于目标值,将搜索范围缩小到左半部分。
重复步骤 2 和 3,直到找到目标值或搜索范围为空。
在下图中为大家展示了二分搜索的过程:
2. 递归实现递归实现二分搜索的代码如下:
1234567891011121314151617181920212223242526272 ...
数据结构
未读1. 串“天行健,君子一自强不息;地势坤,君子以厚德载物”这是《易经》中的原文,对于普通人而言这就是两句话,对于程序员来说这就是一个数据块,是多个相同类型的字符的集合,在数据结构中将其称之为串。
串(String)是由零个或多个字符组成的有限序列,又名叫字符串。一般记作 s=“a1a2a3……an” (n>=0)。其中,s是串的名称,双引号(或单引号)括起来的字符序列是串的值,但是要注意引号不属于串的内容。
空串: 零个字符的串成为空串,它的长度为0,可以用双引号“”表示
串的长度: 串中的字符的数量就是串的总长度
1.1 串的储存结构串的存储结构和线性表相同,分为两种顺序存储结构和链式存储结构。
顺序存储结构:
串的顺序存储结构是用一组地址连续的存储单元(说白了就是数组)来存储串中的字符序列。
大家都学过C语言,此处就不再展开阐述了。
链式存储结构:
对于串的链式存储结构,与线性表相似,但由于串结构的特殊性,结构中的每一个数据元素是一个字符,那么一个链表节点存储一个字符就存在很大的空间浪费,因此可以考虑使用一个节点存储多个字符,最后一个节点如果没有被 ...
1. 用两个栈实现一个队列根据栈的特性,通过一个栈来实现一个队列的行为是做不到的,所以可以再加一个。用两个栈实现一个队列,可以利用栈的后进先出(LIFO)性质,将栈的顺序反转,从而实现队列的先进先出(FIFO)行为。
具体实现方法如下:
定义两个栈:
stack1:用于入队操作。
stack2:用于出队操作
入队操作(enqueue):将新元素压入 stack1。
出队操作(dequeue):
如果 stack2 为空,将 stack1 中的所有元素弹出并压入 stack2。
弹出 stack2 的栈顶元素作为出队元素。
访问队头(front):元素的操作和出队列相似,只是不需要弹出元素。
下图模拟了数据在两个栈(自定义队列)中的移动过程:
通过上面的描述,可以写出如下的C++代码:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374 ...
1. 队列1.1 队列的由来关于常用的受限制的线性表除了栈还有队列。队列与我们的日常生活息息相关,无时无刻都能感受到队列的存在:
早晨起床排队上厕所、洗漱
排队坐地铁、公交上下班,开车也需要排队通过交通路口
排队买早餐,排队在收银口结账,去热门餐厅吃大餐人多还得排队
建设文明和谐的社会需要队列,先进先出、先到先得这是一种公平的体现。由此可见栈、队列都是从日常生活中提炼出的结构化模型,是智慧的结晶。
队列(Queue)作为一种常见的数据结构,遵循先进先出(First In First Out, FIFO)的原则,即最早进入队列的元素最先被移除。队列广泛应用于缓冲区管理、任务调度、消息队列等场景。
和栈一样,队列中也有几个概念需要大家掌握:
队头: 线性表中允许删除数据的一端称为队头
队尾: 线性表中允许插入数据的一端称为队尾
入队列: 将元素添加到队尾的动作叫做入队列
出队列: 将元素从队头删除的动作叫做出队列
空队列: 没有存储任何元素的队列叫空队列,即该线性表是空的
1.2 队列的存储结构因为线性表有两种存储结构顺序存储结构和链式存储结构,所以对于队列而言也有两种存储 ...
在上一个章节中为大家详细讲解了栈的特点和实现,关于栈的现实应用有很多,下面再来给说几个比较常见的案例:括号匹配问题、中缀表达式转后缀表达式、后缀表达式的计算。
1. 括号匹配问题
括号在使用的时候都是成对出现的,分为左右两部分。很多时候我们都需要验证给定的字符串中的括号是否正确匹配,通常包括以下三种类型:
小括号 - ()
大括号 - {}
中括号 - []
如果使用栈来处理这个问题,具体的操作步骤如下:
初始化栈:创建一个空栈,用于存放左括号。
遍历字符串:逐个字符扫描字符串。
如果遇到左括号((、{、[),将其压入栈中。
如果遇到右括号()、}、]),检查栈是否为空:
如果栈为空,说明没有匹配的左括号,匹配失败。
如果栈不为空,从栈顶弹出一个左括号,并检查是否与当前的右括号匹配。如果不匹配,匹配失败。
检查栈:遍历结束后,如果栈不为空,说明有未匹配的左括号,匹配失败;否则,匹配成功。
根据上文的详细描述,我们就可以写出对应的C++代码了:
1234567891011121314151617181920212223242526 ...
1. 栈1.1 栈的由来对于大多数人而言都对生活充满了热爱,如果对身边接触到的各种事物仔细观察就会发现它们有很多相似的特性:
给子弹上弹夹,先压进去的最后被发射出来,最后压进去的第一个被发射出来。
浏览器的后退键,第一次后退看到的是最后浏览的页面,最后一次后退看到的是第一次浏览的页面
带编辑功能的软件,比如:Office、Photoshop、IDE,第一次撤销得到的最后一次修改的内容,最后一次撤销得到的是第一次修改的内容
如果在以上的某一个场景下进行连续的操作,按照线性表的描述我们就可以得到一个从前到后的序列,并且在访问序列中的元素的时候是按照从后往前的顺序进行的。
如果对线性表中元素的访问进行了限制,那么这个线性表就被称作受限制的线性表。常用的受限制的线性表有栈和队列。
栈(Stack)是一种常见的数据结构,它遵循后进先出(Last In First Out,LIFO)的原则,即最新添加的元素最先被移除,也就是它要求仅能在表尾进行元素的插入和删除。
关于栈有几个相关的概念需要大家掌握:
栈顶: 线性表允许插入、删除的一端被称为栈顶
栈底: 线性表不允许插入、删除的一端被称为栈底 ...
数据结构
未读1. 双向循环链表的结构在上一个章节中为大家详细讲解了双向链表,按照单向链表的思路继续对它进行改进,双向链表的首尾就可以相接,这样就得到了一种新的链表 ——双向循环链表。
1.1 双向循环链表的节点双向循环链表是一种特殊的链表结构,链表中的节点不仅有前驱和后继指针,还需要让链表的最后一个节点的后继指针指向第一个节点,第一个节点的前驱指针指向最后一个节点。
假设双向循环链表的节点存储的是整形数据,那么该节点的定义如下:
1234567// 定义一个节点,此为 C++ 语法struct Node{ int data = 0; Node* next = nullptr; Node* prev = nullptr;};
双向循环链表的节点结构包含三个部分:
数据域(data):存储节点的值
前驱指针(prev):指向前一个节点
后继指针(next):指向后一个节点
在操作双向循环链表的时候通常会定义两个辅助指针:头节点指针和尾节点指针,头指针指向链表的第一个节点,尾指针指向链表的最后一个节点。
和前面讲过的链表一样,双向循环链表也可以分为带头 ...
1. 双向链表的结构对于单向链表和单向循环链表而言有一个共同的特点,就是链表的每个节点都只有一个指向后继节点的指针,通过这个指针我们就可以从前往后完成对链表的遍历。但是开弓没有回头箭,遍历到尾节点之后再想要回到头结点,是无能为力的。
1.1 双向链表的节点为了克服链表单向性这一缺点,聪明的程序猿们便进行了改进,设计出了双向链表。双向链表(Doubly Linked List)是一种常见的数据结构,与单向链表不同的是,双向链表中的每个节点包含两个指针,一个指向前驱节点,一个指向后继节点。双向链表的这种特性使得我们可以从任意节点高效地向前或向后遍历。
假设双向链表的节点存储的是整形数据,那么该节点的定义如下:
1234567// 定义一个节点,此为 C++ 语法struct Node{ int data = 0; Node* next = nullptr; Node* prev = nullptr;};
双向链表的节点结构包含三个部分:
数据域(data):存储节点的值
前驱指针(prev):指向前一个节点
后继指针(next):指向后一个节点 ...